Weitere Korpora
- Abkhazian
- Achinese
- Acoli
-
Afrikaans
- Mixed
- News
- Newscrawl
- Web
- Wikipedia
- COM
- Namibia
-
South Africa
-
Web
- 2013 Alle
- 2013 10K
- 2013 30K
- 2013 100K
- 2013 300K
- 2013 1M
- 2014 Alle
- 2015 Alle
- 2015 10K
- 2015 30K
- 2015 100K
- 2015 300K
- 2015 1M
- 2016 Alle
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2019 Alle
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
-
Web
- Akan
- Albanian
- Ambo-Pasco Quechua
- Amharic
- Anaang
-
Arabic
-
News
- 2005-2009 Alle
- 2005-2009 10K
- 2005-2009 30K
- 2005-2009 100K
- 2005-2009 300K
- 2005-2009 1M
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2008 Alle
- 2008 10K
- 2008 30K
- 2008 100K
- 2008 300K
- 2008 1M
- 2009 Alle
- 2009 10K
- 2009 30K
- 2009 100K
- 2009 300K
- 2009 1M
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2013 Alle
- 2015 Alle
- 2015 10K
- 2015 30K
- 2015 100K
- 2015 300K
- 2015 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- Newscrawl
- Web
- Wikipedia
- Algeria
- Australia
- Bahrain
- COM
- Canada
- China, People's Republic of
- Egypt
- France
- Germany
- Iran
- Iraq
- Jordan
- Kuwait
- Lebanon
- Libya
- Mauritania
- Morocco
- Oman
- Palestine
- Qatar
- Russia
- Saudi Arabia
- Sudan
- Sweden
- Syria
- Tunisia
- Turkey
- United Arab Emirates
- United Kingdom
- Yemen
-
News
- Aragonese
- Armenian
- Arpitan
- Asháninka
- Assamese
- Assyrian Neo-Aramaic
- Asturian
- Atikamekw
- Avaric
- Aymara
- Azerbaijani
- Balinese
- Balkan Romani
- Bambara
- Banjar
- Bashkir
- Basque
- Bavarian
- Belarusian
- Bengali
- Betawi
- Bihari
- Bikol
- Bishnupriya
- Bislama
- Bosnian
- Breton
- Buginese
-
Bulgarian
-
News
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2008 Alle
- 2009 Alle
- 2010 Alle
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2013 Alle
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- Newscrawl
- Web
-
Wikipedia
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2012 Alle
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2014 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- Bulgaria
- COM
- European Union
-
News
- Buriat
- Burmese
- Candoshi-Shapra
- Catalan
- Cebuano
- Central Aymara
- Central Bikol
- Central Khmer
- Central Kurdish
- Central Mazahua
- Chamorro
- Chavacano
- Chechen
- Cherokee
- Cheyenne
- Chinese
- Choctaw
- Chol
- Church Slavic
- Chuukese
- Chuvash
- Classical Nahuatl
- Cornish
- Corsican
- Cree
- Crimean Tatar
- Croatian
-
Czech
- Mixed
-
News
- 2005 Alle
- 2005 10K
- 2005 30K
- 2005-2007 Alle
- 2005-2007 10K
- 2005-2007 30K
- 2005-2007 100K
- 2005-2007 300K
- 2005-2007 1M
- 2007 Alle
- 2008 Alle
- 2009 Alle
- 2010 Alle
- 2011 Alle
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2012 1M
- 2013 Alle
- 2013 10K
- 2013 30K
- 2013 100K
- 2013 300K
- 2013 1M
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2021 30K
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
-
Newscrawl
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2013 Alle
- 2013 10K
- 2013 30K
- 2013 100K
- 2013 300K
- 2013 1M
- 2015 Alle
- 2015 10K
- 2015 30K
- 2015 100K
- 2015 300K
- 2015 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- Web
-
Wikipedia
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2010 Alle
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2012 1M
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2014 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- COM
- Czech Republic
- European Union
-
Danish
-
News
- 2005 Alle
- 2006 Alle
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2007 1M
- 2008 Alle
- 2008 10K
- 2008 30K
- 2008 100K
- 2008 300K
- 2009 Alle
- 2010 Alle
- 2011 Alle
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2012 1M
- 2013 Alle
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
-
Newscrawl
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2013 Alle
- 2015 Alle
- 2015 10K
- 2015 30K
- 2015 100K
- 2015 300K
- 2015 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
- Web
-
Wikipedia
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2014 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- COM
- Denmark
- European Union
- Faroe Islands
- Greenland
-
News
- Dari
- Dhivehi
- Dimli
- Dinka
- Dotyali
-
Dutch
-
News
- 2005 Alle
- 2005 10K
- 2005 30K
- 2005 100K
- 2006 Alle
- 2006 10K
- 2006 30K
- 2006 100K
- 2006 300K
- 2007 Alle
- 2008 Alle
- 2009 Alle
- 2009 10K
- 2009 30K
- 2009 100K
- 2009 300K
- 2009 1M
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2013 Alle
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
- Newscrawl
- Web
- Wikipedia
- Aruba
- Belgium
- COM
- European Union
- Netherlands
- Netherlands Antilles
- South Africa
- Suriname
-
News
- Dzongkha
- Eastern Canadian Inuktitut
- Eastern Mari
- Eastern Yiddish
- Egyptian Arabic
- Emiliano-Romagnolo
-
English
-
News
- 2005 Alle
- 2005 10K
- 2005 30K
- 2005 100K
- 2005 300K
- 2005 1M
- 2006 Alle
- 2006 10K
- 2006 30K
- 2006 100K
- 2006 300K
- 2006 1M
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2007 1M
- 2008 Alle
- 2008 10K
- 2008 30K
- 2008 100K
- 2008 300K
- 2008 1M
- 2009 Alle
- 2009 10K
- 2009 30K
- 2009 100K
- 2009 300K
- 2009 1M
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2012 1M
- 2013 Alle
- 2013 10K
- 2013 30K
- 2013 100K
- 2013 300K
- 2013 1M
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2014 1M
- 2015 Alle
- 2015 10K
- 2015 30K
- 2015 100K
- 2015 300K
- 2015 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2021 10K
- 2021 30K
- 2021 300K
- 2021 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
- 2024 Alle
- 2024 10K
- 2024 30K
- 2024 100K
- 2024 300K
- 2024 1M
- Newscrawl
- Newscrawl-part
- Newscrawl-public
- Web
- Wikipedia
- American Samoa
- Anguilla
- Antigua and Barbuda
- Ascension
- Australia
- Bahamas, The
- Barbados
- Bermuda
- Botswana
- British Indian Ocean Territory
- Brunei
- COM
- Cambodia
- Canada
- Cayman Islands
- Dominica
- EDU
- European Union
- Falkland Islands (Islas Malvinas)
- Fiji
- GAMES
- GOV
- Gambia, The
- Germany
- Gibraltar
- Guadeloupe
- Guam
- Guernsey
- Guyana
- India
- Indonesia
- Ireland
- Isle of Man
- Jamaica
- Jersey
- Kiribati
- Montserrat
- NET
- Namibia
- Nauru
- New Zealand
- Niue
- Norfolk Island
- Pakistan
- Philippines
- Puerto Rico
- Saint Kitts and Nevis
- Saint Lucia
- Saint Pierre and Miquelon
- Saint Vincent and the Grenadines
- Samoa
- Seychelles
- Singapore
- South Africa
- South Georgia & South Sandwich Islands
- Thailand
- Tokelau
- Turks and Caicos Islands
- United Kingdom
- United States
- Zambia
- Zimbabwe
-
News
- Erzya
-
Esperanto
- Mixed
- Newscrawl
- Web
-
Wikipedia
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- European Union
-
Estonian
-
News
- Alle
- 2005 Alle
- 2006 Alle
- 2007 Alle
- 2008 Alle
- 2009 Alle
- 2010 Alle
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2012 Alle
- 2013 Alle
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- Newscrawl
- Web
- Wikipedia
- COM
- Estonia
- European Union
-
News
- Even
- Ewe
- Extremaduran
- FRI
- Faroese
- Fiji Hindi
- Fijian
-
Finnish
-
News
- 2005 Alle
- 2005 10K
- 2005 30K
- 2005-2007 Alle
- 2005-2007 10K
- 2005-2007 30K
- 2005-2007 100K
- 2005-2007 300K
- 2006 Alle
- 2006 10K
- 2006 30K
- 2006 100K
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2008 Alle
- 2009 Alle
- 2010 Alle
- 2011 Alle
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2013 Alle
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- Newscrawl
- Web
-
Wikipedia
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2007 1M
- 2010 Alle
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2012 1M
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2014 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- COM
- European Union
- Finland
- Sweden
-
News
-
French
- Mixed
-
News
- 2002-2005 Alle
- 2002-2005 10K
- 2002-2005 30K
- 2002-2005 100K
- 2002-2005 300K
- 2002-2005 1M
- 2005 Alle
- 2005 10K
- 2005 30K
- 2005 100K
- 2005 300K
- 2005 1M
- 2005-2008 Alle
- 2005-2008 10K
- 2005-2008 30K
- 2005-2008 100K
- 2005-2008 300K
- 2005-2008 1M
- 2006 Alle
- 2006 10K
- 2006 30K
- 2006 100K
- 2006 300K
- 2006 1M
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2007 1M
- 2008 Alle
- 2008 10K
- 2008 30K
- 2008 100K
- 2008 300K
- 2008 1M
- 2009 Alle
- 2009 10K
- 2009 30K
- 2009 100K
- 2009 300K
- 2009 1M
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2012 10K
- 2013 Alle
- 2013 10K
- 2013 30K
- 2013 100K
- 2013 300K
- 2013 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2021 Alle
- 2021 30K
- 2021 100K
- 2021 300K
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
- 2024 Alle
- 2024 10K
- 2024 30K
- 2024 100K
- 2024 300K
- 2024 1M
-
Newscrawl
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2014 1M
- 2015 Alle
- 2015 10K
- 2015 30K
- 2015 100K
- 2015 300K
- 2015 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2021 Alle
- Newscrawl-public
- Web
-
Wikipedia
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2007 1M
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2012 1M
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2014 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- Algeria
- Belgium
- Benin
- Burkina Faso
- Burundi
- COM
- Cameroon
- Canada
- Congo, (Congo & Brazzaville)
- Congo, (Congo & Kinshasa)
- Cote d'Ivoire (Ivory Coast)
- European Union
- France
- French Polynesia
- Gabon
- Guadeloupe
- Guinea
- Haiti
- Jersey
-
Luxembourg
-
Web
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2012 Alle
- 2012 10K
- 2012 30K
- 2013 Alle
- 2013 10K
- 2013 30K
- 2013 100K
- 2013 300K
- 2013 1M
- 2015 Alle
- 2015 10K
- 2015 30K
- 2015 100K
- 2015 300K
- 2015 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2021 Alle
-
Web
- Madagascar
- Mali
- Martinique
- Monaco
- New Caledonia
- Niger
- Reunion
- Rwanda
- Saint Pierre and Miquelon
- Senegal
-
Switzerland
-
Web
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2012 1M
- 2013 Alle
- 2013 10K
- 2013 30K
- 2013 100K
- 2013 300K
- 2013 1M
- 2015 Alle
- 2015 10K
- 2015 30K
- 2015 100K
- 2015 300K
- 2015 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2022 Alle
-
Web
- Togo
- Tuvalu
- Friulian
- Fulah
- Ga
- Gagauz
- Galician
- Gan Chinese
- Ganda
- Georgian
-
German
- Easynews
-
News
- 1995 Alle
- 1995 10K
- 1995 30K
- 1995 100K
- 1995 300K
- 1995 1M
- 1996 Alle
- 1996 10K
- 1996 30K
- 1996 100K
- 1996 300K
- 1996 1M
- 1997 Alle
- 1997 10K
- 1997 30K
- 1997 100K
- 1997 300K
- 1997 1M
- 1998 Alle
- 1998 10K
- 1998 30K
- 1998 100K
- 1998 300K
- 1998 1M
- 1999 Alle
- 1999 10K
- 1999 30K
- 1999 100K
- 1999 300K
- 1999 1M
- 2000 Alle
- 2000 10K
- 2000 30K
- 2000 100K
- 2000 300K
- 2000 1M
- 2001 Alle
- 2001 10K
- 2001 30K
- 2001 100K
- 2001 300K
- 2001 1M
- 2002 Alle
- 2002 10K
- 2002 30K
- 2002 100K
- 2002 300K
- 2002 1M
- 2003 Alle
- 2003 10K
- 2003 30K
- 2003 100K
- 2003 300K
- 2003 1M
- 2004 Alle
- 2004 10K
- 2004 30K
- 2004 100K
- 2004 300K
- 2004 1M
- 2005 Alle
- 2005 10K
- 2005 30K
- 2005 100K
- 2005 300K
- 2005 1M
- 2006 Alle
- 2006 10K
- 2006 30K
- 2006 100K
- 2006 300K
- 2006 1M
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2007 1M
- 2008 Alle
- 2008 10K
- 2008 30K
- 2008 100K
- 2008 300K
- 2008 1M
- 2009 Alle
- 2009 10K
- 2009 30K
- 2009 100K
- 2009 300K
- 2009 1M
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2012 1M
- 2013 Alle
- 2013 10K
- 2013 30K
- 2013 100K
- 2013 300K
- 2013 1M
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2014 1M
- 2015 Alle
- 2015 10K
- 2015 30K
- 2015 100K
- 2015 300K
- 2015 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
- 2024 Alle
- 2024 10K
- 2024 30K
- 2024 100K
- 2024 300K
- 2024 1M
- Newscrawl
- Newscrawl-hyphen
- Newscrawl-part00
- Newscrawl-part01
- Newscrawl-part02
- Newscrawl-public
- Web
-
Wikipedia
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2007 1M
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2012 1M
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2014 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- Ascension
- Austria
- Belgium
- COM
- European Union
- Germany
- Hungary
- Italy
- Liechtenstein
- Luxembourg
- Namibia
- Poland
- South Africa
- Switzerland
- ZZ
- Gheg Albanian
- Gilaki
- Goan Konkani
- Gorontalo
- Gothic
- Guarani
- Gujarati
- Güilá Zapotec
- Haitian
- Hakka Chinese
- Halh Mongolian
- Hausa
- Hawaiian
-
Hebrew
-
News
- 2007 Alle
- 2008 Alle
- 2008 10K
- 2008 30K
- 2008 100K
- 2008 300K
- 2008 1M
- 2009 Alle
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2013 Alle
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- Newscrawl
- Web
-
Wikipedia
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2012 1M
- 2014 Alle
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- COM
- Israel
-
News
- Hiligaynon
-
Hindi
-
News
- 2007 Alle
- 2007 10K
- 2007 30K
- 2008 Alle
- 2008 10K
- 2008 30K
- 2008 100K
- 2009 Alle
- 2009 10K
- 2009 30K
- 2009 100K
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2013 Alle
- 2014 Alle
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- Newscrawl
- Web
-
Wikipedia
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2010 Alle
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- COM
- India
-
News
- Hmong Don
- Hungarian
- Iban
- Icelandic
- Ido
- Igbo
- Iloko
-
Indonesian
- Mixed
-
News
- 2007 Alle
- 2008 Alle
- 2008 10K
- 2008 30K
- 2008 100K
- 2008 300K
- 2009 Alle
- 2009 10K
- 2009 30K
- 2009 100K
- 2009 300K
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2013 Alle
- 2014 Alle
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
- Newscrawl
- Newscrawl-tufs5
- Newscrawl-tufs6
- Web
-
Wikipedia
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2014 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- Brunei
- COM
- India
- Indonesia
- Ingush
- Interlingua
- Interlingue
- Inuktitut
- Inupiaq
- Iranian Persian
- Irish
-
Italian
-
News
- 2002 Alle
- 2005 Alle
- 2005 10K
- 2005 30K
- 2005 100K
- 2005 300K
- 2005 1M
- 2005-2009 Alle
- 2005-2009 10K
- 2005-2009 30K
- 2005-2009 100K
- 2005-2009 300K
- 2005-2009 1M
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2008 Alle
- 2008 10K
- 2008 30K
- 2008 100K
- 2008 300K
- 2008 1M
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2012 10K
- 2012 100K
- 2012 1M
- 2013 Alle
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
-
Newscrawl
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2015 Alle
- 2015 10K
- 2015 30K
- 2015 100K
- 2015 300K
- 2015 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2018 Alle
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2021 Alle
- Web
-
Wikipedia
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2014 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- COM
- European Union
- Italy
- Malta
- San Marino
- Slovenia
-
Switzerland
-
Web
- 2011 Alle
- 2013 Alle
- 2015 Alle
- 2015 10K
- 2015 30K
- 2015 100K
- 2015 300K
- 2015 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2018 Alle
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2022 Alle
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
-
Web
- Vatican City
-
News
- Ivatan
- Jamaican Creole English
-
Japanese
-
News
- 2005 Alle
- 2005 10K
- 2005 30K
- 2005 100K
- 2005 300K
- 2005-2008 Alle
- 2005-2008 10K
- 2005-2008 30K
- 2005-2008 100K
- 2005-2008 300K
- 2005-2008 1M
- 2007 Alle
- 2008 Alle
- 2008 10K
- 2008 30K
- 2008 100K
- 2008 300K
- 2009 Alle
- 2009 10K
- 2009 30K
- 2009 100K
- 2009 300K
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2013 Alle
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2021 Alle
- 2021 10K
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- Newscrawl
- Web
- Wikipedia
- COM
- Japan
-
News
- Javanese
- Kabardian
- Kabiyè
- Kabyle
- Kalaallisut
- Kalmyk
- Kamayo
- Kannada
- Kara-Kalpak
- Karachay-Balkar
- Kashmiri
- Kashubian
- Kazakh
- Kekchí
- Khasi
- Kikuyu
- Kinyarwanda
- Kirghiz
- Kituba (Congo)
- Klingon
- Komi
- Komi-Permyak
- Konkani
- Koongo
-
Korean
-
News
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2007 1M
- 2008 Alle
- 2008 10K
- 2008 30K
- 2008 100K
- 2008 300K
- 2008 1M
- 2009 Alle
- 2009 10K
- 2009 30K
- 2009 100K
- 2009 300K
- 2009 1M
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2013 Alle
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- Newscrawl
- Web
-
Wikipedia
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2012 1M
- 2014 Alle
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- COM
- Japan
- Korea, South
-
News
- Kurdish
- Kölsch
- LNC
- Ladino
- Lak
- Lao
- Latgalian
- Latin
- Latvian
- Lezghian
- Ligurian
- Limburgan
- Lingala
- Lithuanian
- Logudorese Sardinian
- Lojban
- Loke
- Lombard
- Low German
- Lower Sorbian
- Lumbu
- Luo (Cameroon)
- Lushai
- Luxembourgish
- MLY
- Macedo-Romanian
- Macedonian
- Madurese
- Maithili
- Malagasy
- Malay
- Malayalam
- Maltese
- Mandarin Chinese
- Manx
- Maori
- Marathi
- Marshallese
- Mazanderani
- Mi'kmaq
- Middle High German (ca. 1050-1500)
- Min Dong Chinese
- Min Nan Chinese
- Minangkabau
- Mingrelian
- Mirandese
-
Modern Greek
-
News
- 2007 Alle
- 2007 10K
- 2007 30K
- 2008 Alle
- 2009 Alle
- 2010 Alle
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2012 Alle
- 2013 Alle
- 2013 10K
- 2013 30K
- 2013 100K
- 2013 300K
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
-
Newscrawl
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2012 1M
- 2013 Alle
- 2013 10K
- 2013 30K
- 2013 100K
- 2013 300K
- 2013 1M
- 2015 Alle
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2019 Alle
- 2021 Alle
- Web
-
Wikipedia
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2012 Alle
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- COM
- Cyprus
- European Union
- Greece
-
News
- Moksha
- Mongolian
- Mozarabic
- Mískito
- Nahuatl
- Nauru
- Navajo
- Ndonga
- Neapolitan
- Nepali
- Newari
- Nias
- Nigerian Pidgin
- North Azerbaijani
- North Ndebele
- Northern Frisian
- Northern Kurdish
- Northern Luri
- Northern Sami
- Northern Uzbek
- Norwegian
- Norwegian Bokmål
-
Norwegian Nynorsk
- Newscrawl
- Web
-
Wikipedia
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- Norway
- Novial
- Nyanja
- Nyankole
- Occitan
- Ojitlán Chinantec
- Old English
- Old Norse
- Oriya
- Oromo
- Ossetian
- PRV
- Palauan
- Pali
- Pampanga
- Pangasinan
- Panjabi
- Papiamento
- Pedi
- Pennsylvania German
-
Persian
- News
-
Newscrawl
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2013 Alle
- 2013 10K
- 2013 30K
- 2013 100K
- 2013 300K
- 2013 1M
- 2015 Alle
- 2015 10K
- 2015 30K
- 2015 100K
- 2015 300K
- 2015 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- Web
- Wikipedia
- COM
- Iran
- Pfaelzisch
- Picard
- Piemontese
- Pijin
- Pitcairn-Norfolk
- Plateau Malagasy
- Pohnpeian
-
Polish
-
News
- 2005 Alle
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2007 1M
- 2008 Alle
- 2008 10K
- 2008 30K
- 2008 100K
- 2008 300K
- 2008 1M
- 2009 Alle
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2013 Alle
- 2013 10K
- 2013 30K
- 2013 100K
- 2013 300K
- 2013 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
-
Newscrawl
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2013 Alle
- 2015 Alle
- 2015 10K
- 2015 30K
- 2015 100K
- 2015 300K
- 2015 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2019 Alle
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- Web
-
Wikipedia
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2007 1M
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2014 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- COM
- European Union
- Poland
-
News
- Pontic
-
Portuguese
-
News
- 2005 Alle
- 2006 Alle
- 2007 Alle
- 2008 Alle
- 2009 Alle
- 2010 Alle
- 2011 Alle
- 2012 Alle
- 2013 Alle
- 2013 10K
- 2013 30K
- 2013 100K
- 2013 300K
- 2013 1M
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
- Newscrawl
- Web
- Wikipedia
- Angola
- Brazil
- COM
- Cape Verde
- European Union
- Luxembourg
- Macau
- Mozambique
- Netherlands Antilles
- Portugal
-
News
- Pulaar
- Pushto
- Páez
- Quechua
- Romance
-
Romanian
-
News
- 1998-2007 Alle
- 1998-2007 10K
- 1998-2007 30K
- 1998-2007 100K
- 1998-2007 300K
- 1998-2007 1M
- 2005 Alle
- 2007 Alle
- 2008 Alle
- 2009 Alle
- 2010 Alle
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2012 Alle
- 2013 Alle
- 2015 Alle
- 2015 10K
- 2015 30K
- 2015 100K
- 2015 300K
- 2015 1M
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- Newscrawl
- Web
- Wikipedia
- COM
- European Union
- Moldova
- Romania
-
News
- Romansh
- Romany
- Roria
- Rundi
- Russia Buriat
-
Russian
- Mixed
-
News
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2007 1M
- 2008 Alle
- 2009 Alle
- 2009 10K
- 2009 30K
- 2009 100K
- 2009 300K
- 2009 1M
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2012 Alle
- 2013 Alle
- 2013 10K
- 2013 30K
- 2013 100K
- 2013 300K
- 2013 1M
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
- Newscrawl
- Newscrawl-public
- Web
-
Wikipedia
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2014 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- Armenia
- Azerbaijan
- Belarus
- COM
- Estonia
- European Union
- Georgia
- Israel
- Kazakhstan
- Kyrgyzstan
- Latvia
- Lithuania
- Moldova
- Russia
- SU
- Tajikistan
- Turkmenistan
- Tuvalu
- Ukraine
- Uzbekistan
- Rusyn
- Sami
- Samoan
- Samogitian
- San Blas Kuna
- Sango
- Sanskrit
- Sardinian
- Saterfriesisch
- Scots
- Scottish Gaelic
- Seraiki
- Serbian
- Serbo-Croatian
- Seselwa Creole French
- Shona
- Sicilian
- Silesian
- Sindhi
- Sinhala
- Slovak
- Slovenian
- Somali
- South Azerbaijani
- South Ndebele
- Southern Altai
- Southern Aymara
- Southern Sotho
-
Spanish
-
News
- 2001-2002 Alle
- 2001-2002 10K
- 2001-2002 30K
- 2001-2002 100K
- 2001-2002 300K
- 2001-2002 1M
- 2005 Alle
- 2006 Alle
- 2006 10K
- 2006 30K
- 2006 100K
- 2006 300K
- 2006 1M
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2007 1M
- 2008 Alle
- 2008 10K
- 2008 30K
- 2008 100K
- 2008 300K
- 2008 1M
- 2009 Alle
- 2009 10K
- 2009 30K
- 2009 100K
- 2009 300K
- 2009 1M
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2012 1M
- 2013 Alle
- 2013 10K
- 2013 30K
- 2013 100K
- 2013 300K
- 2013 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2017 Alle
- 2017 10K
- 2017 30K
- 2017 100K
- 2017 300K
- 2017 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
- 2024 Alle
- 2024 10K
- 2024 30K
- 2024 100K
- 2024 300K
- 2024 1M
- Newscrawl
- Newscrawl-public
- Web
-
Wikipedia
- 2010 Alle
- 2010 10K
- 2010 30K
- 2010 100K
- 2010 300K
- 2010 1M
- 2011 Alle
- 2011 10K
- 2011 30K
- 2011 100K
- 2011 300K
- 2011 1M
- 2014 Alle
- 2014 10K
- 2014 30K
- 2014 100K
- 2014 300K
- 2014 1M
- 2016 Alle
- 2016 10K
- 2016 30K
- 2016 100K
- 2016 300K
- 2016 1M
- 2018 Alle
- 2018 10K
- 2018 30K
- 2018 100K
- 2018 300K
- 2018 1M
- 2021 Alle
- 2021 10K
- 2021 30K
- 2021 100K
- 2021 300K
- 2021 1M
- Andorra
- Argentina
- Bolivia
- COM
- Chile
- Colombia
- Costa Rica
- Cuba
- Dominican Republic
- Ecuador
- El Salvador
- European Union
- Gibraltar
- Guatemala
- Honduras
- Mexico
- Nicaragua
- Panama
- Paraguay
- Peru
- Puerto Rico
- Spain
- United States
- Uruguay
- Venezuela
-
News
- Sranan Tongo
- Standard Arabic
- Standard Estonian
- Standard Latvian
- Standard Malay
- Sundanese
- Swahili
- Swati
-
Swedish
-
News
- 2005 Alle
- 2005 10K
- 2005 30K
- 2005 100K
- 2005 300K
- 2005 1M
- 2006 Alle
- 2006 10K
- 2006 30K
- 2006 100K
- 2006 300K
- 2007 Alle
- 2007 10K
- 2007 30K
- 2007 100K
- 2007 300K
- 2007 1M
- 2008 Alle
- 2009 Alle
- 2010 Alle
- 2011 Alle
- 2012 Alle
- 2012 10K
- 2012 30K
- 2012 100K
- 2012 300K
- 2013 Alle
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
- Newscrawl
- Web
- Wikipedia
- COM
- European Union
- Finland
- Sweden
-
News
- Swiss German
- Tabasco Nahuatl
- Tagalog
- Tahitian
- Tajik
- Tama (Colombia)
- Tamil
- Tatar
- Tay Khang
- Tedim Chin
- Telugu
- Tena Lowland Quichua
- Tetum
- Thai
- Tibetan
- Tigrinya
- Tiv
- Tok Pisin
- Tokelau
- Tonga (Tonga Islands)
- Tosk Albanian
- Tsimihety Malagasy
- Tsonga
- Tswana
- Tulu
- Tumbuka
-
Turkish
-
News
- 2005 Alle
- 2005 10K
- 2005 30K
- 2005 100K
- 2005 300K
- 2005 1M
- 2007 Alle
- 2008 Alle
- 2009 Alle
- 2010 Alle
- 2011 Alle
- 2012 Alle
- 2013 Alle
- 2019 Alle
- 2019 10K
- 2019 30K
- 2019 100K
- 2019 300K
- 2019 1M
- 2020 Alle
- 2020 10K
- 2020 30K
- 2020 100K
- 2020 300K
- 2020 1M
- 2022 Alle
- 2022 10K
- 2022 30K
- 2022 100K
- 2022 300K
- 2022 1M
- 2023 Alle
- 2023 10K
- 2023 30K
- 2023 100K
- 2023 300K
- 2023 1M
- Newscrawl
- Web
- Wikipedia
- Bulgaria
- COM
- Cyprus
- European Union
- Turkey
-
News
- Turkmen
- Tuvinian
- Twi
- Tzeltal
- Tzotzil
- Udmurt
- Uighur
- Ukrainian
- Upper Guinea Crioulo
- Upper Sorbian
- Urdu
- Uzbek
- Venda
- Venetian
- Vietnamese
- Vlaams
- Vlax Romani
- Volapük
- Võro
- Walloon
- Waray (Philippines)
- Wayana
- Welsh
- West Central Oromo
- Western Frisian
- Western Mari
- Western Panjabi
- Wolof
- Wu Chinese
- Xhosa
- Yakut
- Yiddish
- Yoruba
- Yue Chinese
- Zeeuws
- Zhuang
- Zulu
The most frequent word beginnings as character N-grams for N=1...5 with Zipf's diagram
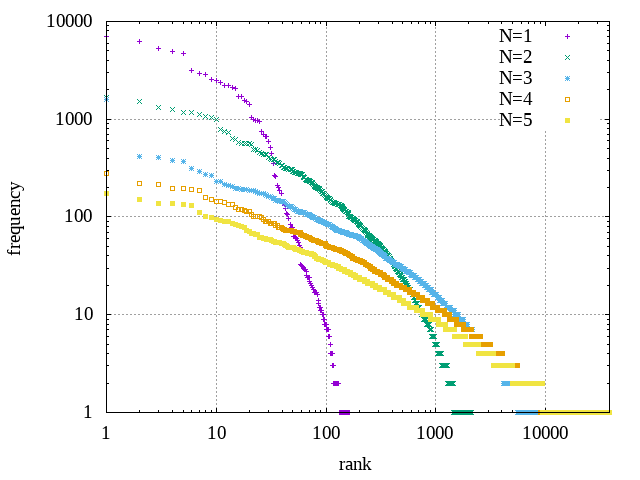
Zipf's diagram for word beginnings
Top Characters
| word rank | frequency | n-gram |
|---|---|---|
| 1 | 7069 | स- |
| 2 | 6255 | प- |
| 3 | 5242 | क- |
| 4 | 4952 | म- |
| 5 | 4686 | व- |
Top Character Bigrams
| word rank | frequency | n-gram |
|---|---|---|
| 1 | 1688 | प्- |
| 2 | 1504 | वि- |
| 3 | 1308 | का- |
| 4 | 1265 | स्- |
| 5 | 1177 | मा- |
Top Character Trigrams
| word rank | frequency | n-gram |
|---|---|---|
| 1 | 1600 | प्र- |
| 2 | 414 | राज- |
| 3 | 406 | स्व- |
| 4 | 377 | महा- |
| 5 | 373 | व्य- |
Top Character 4-Grams
| word rank | frequency | n-gram |
|---|---|---|
| 1 | 276 | त्या- |
| 2 | 221 | प्रत- |
| 3 | 217 | प्रा- |
| 4 | 195 | कार्- |
| 5 | 194 | चित्- |
Top Character 5-Grams
| word rank | frequency | n-gram |
|---|---|---|
| 1 | 176 | चित्र- |
| 2 | 151 | इ.स.- |
| 3 | 139 | कार्य- |
| 4 | 139 | प्रति- |
| 5 | 135 | विद्य- |
2.2.5 Most frequent word beginnings
Data Description
The tables show the most frequent letter-N-grams at the beginning of words for N=1…5. Their frequency is count without multiplicity, otherwise the stopwords would dominate the tables.
As shown in the above example (German), word prefixes are clearly visible. In the above example, ver- and ein- are prefixes, and Sch- is not. At the end of a prefix we typically have a wide variety of possible continuations. Hence a prefix of length k will be prominent in the table for N=k, but typically not in the table for N=k+1. The prominent entries Schw- and Schl- for N=4 tell us that Sch- is no prefix.
Zipf’s diagram is plotted with both axis in logarithmic scale, hence we expect nearly straight lines. The graphs look more typical for larger N. Especially for N=3 we find only a small number of trigrams resulting in a sharp decay.
Usage
For a language unknown to the reader, the data can easily be used to see whether prefixes do exist and to find the most prominent examples.
Technical Details
For counting, only words with a minimum character length of 10 were considered.
Because only a word list is needed, the tables above can be generated from a relatively small corpus.
Simplified Select statement
For N=3:
SELECT @pos:=(@pos+1), xx.* from (SELECT @pos:=0) r, (select count(*) as cnt, concat(left(word,3),"-") FROM words WHERE w_id>100 group by left(word,3) order by cnt desc) xx limit 5;
Open questions
-
For more insight in a language, longer lists might be useful.
-
Is there a need for larger N
See also
-
Most frequent word endings
-
Most frequent letter-N-grams
-
Number of letter-N-Grams at word beginnings
-
Number of letter-N-Grams at word endings